אלגברה, פרק 13: תחום וטווח של יחסים בינריים
בסרטון הזה נכיר את התחום והטווח של יחסים בינריים – שתי קבוצות רבות חשיבות כשעוסקים ביחסים בינריים, וכמו שנראה בהמשך הסדרה הן חשובות מאוד גם כשעוסקים בפונקציות.
צפה בסרטון
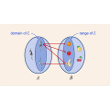
האם כל האיברים מהקבוצות A,B חייבים להופיע בתוך הזוגות הסדורים שמרכיבים את הקבוצה L ?בחרו בתשובה הנכונה.
אין מספיק נתונים כדי להשיב על השאלה.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
אין הגבלה על מספר האיברים מכל קבוצה.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
כן.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
חייב להופיע לפחות איבר אחד מכל קבוצה (A,B).
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
חייבים להופיע כל איברי קבוצה B, אין הגבלה על קבוצה A.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
חייבים להופיע כל איברי קבוצה A, אין הגבלה על קבוצה B.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
התאימו בין המושג שבטור א להגדרתו שבטור ב.
נסמן D=תחום, R=טווח. מה הקשר בין מספר האיברים בתחום $(|D|)$ ובטווח $(|R|)$ לבין מספר האיברים בקבוצות A.B (כלומר $|A|,|B|$)? בחרו בתשובות הנכונות.
$|D|<|A|$ , $|B| leq |R|$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
$|D| leq |A|$ , $|B| leq |R|$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
$|D| leq |A|$ , $|R| leq |B|$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
$|D|<|A|$ , $|R|<|B|$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
$|R|<|A|$ , $|D|<|B|$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
$|R| leq |B|$ , $|D| leq |A|$
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
מה יכולים להיות התחום והטווח של יחס בינארי בין $mathbb{R} $ ל- $mathbb{R}$ ? האם יכול להיוץ מספר ממשי שאינו כלול בתחום של היחס הזה?
שיבוץ האיברים של L בתוך מערכת צירים יכול לעזור לנו להבחין אם היחס L מהווה פונקציה או לא. מבחן הקו האנכי הוא כלי ויזואלי פשוט ושימושי. עם זאת, חשוב לזכור שניתן לשרטט גרפים גם עבור התאמות שאינן פונקציות.
שימוש בתרשימי פיזור נפוץ מאוד לשם זיהוי דפוסים באוספים גדולים של נתונים. למשל, בזיהוי מגמות הקשורות להתנהגות של אוכלוסיות. ראו למשל את הסרטון "פירמידות אוכלוסייה" בכתבה באתר מכון דוידסון:http://bit.ly/2o0vvjI
תחום וטווח של התאמות ‒ סרטון אינטראקטיבי
הפעל סרטוןעל הפעילות
בסרטון זה התלמידים ילמדו על התחום והטווח של התאמות (ובפרט פונקציות) בין קבוצות. בפרט, הם יראו מהם קטעים חסומים (סגורים/פתוחים). השאלות דורשות גם יישום ידע קודם עם המידע מהסרטון. משך הפעילות הוא כ-20 דקות.
תחום, טווח, התאמה, פונקציה, משתנה תלוי, משתנה בלתי תלוי
חוקרים: תחום וטווח בחלל - חט"ב/חט"ע
על הפעילות
בפעילות זו התלמידים ינתחו את שיגור החללית "בראשית", וילמדו על משמעות הנתונים המוצגים על המסך ועל קשרים ביניהם. לשם כך יעבדו התלמידים בצוותים. פעילות זו מיועדת לפתיחת הנושא "תחום וטווח של פונקציה", ומספקת גם העשרה לגבי המושגים המתאימים מתורת הקבוצות.
תחום, טווח, התאמה, פונקציה, משתנה תלוי, משתנה בלתי תלוי
בניית טיעון, הבניית ידע, יצירתיות, שיתוף פעולה
תכנים נוספים שעשויים לעניין אותך
המגן הירוק של העולם עולה באש
יער האמזונס בברזיל מצטמצם בהתמדה מאז שנות ה-70, וההשלכות על האקלים העולמי והכלכלה עלולות להיות הרות גורל. בחירות המבוססות על ראיות מדעיות יכולות למנוע קטסטרופה
השיר הוויראלי של הדרורים האמריקאיים
סגנון חדש של שירה סחף את הדרורים לבני הצוואר והתפשט ברחבי קנדה תוך פחות מ-20 שנה.
הגנים שהעלו אותנו ליבשה
מחקר חדש מראה כיצד הגנום הענקי של דגי הריאות עזר לקרוביהם הקדומים לעשות את המעבר מהחיים בים ליבשה