Dreidimensionale geometrische Ornamente
Der Mathematiker und Künstler George Hart zeigt in diesem Videofilm, wie man aus Papier sieben farbige geometrische Modelle bauen kann. Jedes Modell setzt sich aus gleichen regelmäßigen Vielecken zusammen: Dreiecken, Quadraten, Fünfecken, Sechsecken, Zehnecken und Sternen. Jeder Teil hat Schlitze, die es erlauben, die verschiedenen Teile ineinander zu verhaken und sie so ohne Verwendung von Klebstoff oder Stecknadeln zu verbinden. Anhand des Videofilms und der unten stehenden Anleitungen und Vorlagen kannst du die Modelle bauen. Ansehen, bauen und die Früchte des Fleißes genießen!
צפה בסרטון
Was ist ein regelmäßiges Vieleck? Wähle die richtige Antwort.
Ein Vieleck, bei dem alle Seiten gleich lang und alle Winkel gleich groß sind.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Ein besonderes, nicht einfaches Vieleck, zum Beispiel ein Sechseck.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Ein Vieleck, das kein Dreieck ist.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Der gezeigte dreidimensionale Körper ist ein regelmäßiges Ikosaeder. Aus wie vielen und welchen Vielecken ist es zusammengesetzt? Wähle die richtige Antwort.
Zwanzig Seitenflächen, von denen jede ein regelmäßiges Dreieck ist.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Zwanzig Seitenflächen, von denen jede ein beliebiges Dreieck ist.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Viele Seitenflächen, von denen jede ein regelmäßiges Dreieck ist.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Zehn Seitenflächen, von denen jede ein gleichschenkeliges Dreieck ist.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Was ist die Summe der Winkel, die von den Dreiecken rund um jeden Eckpunkt gebildet werden? Wähle die richtige Antwort
Wie immer rund um jeden Punkt
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Sie werden durch drei Eckpunkte von drei nebeneinander liegenden regelmäßigen Dreiecken gebildet.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Sie ist gleich der Winkelsumme eines regelmäßigen Dreiecks.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Sie werden durch zwei Eckpunkte von zwei nebeneinander liegenden regelmäßigen Dreiecken gebildet.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Wie in dem Video zu sehen, kann man einen Würfel erkennen, dessen Eckpunkte durch die Punkte gebildet werden, an denen die Seiten der Dreiecke
2 Würfel
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
3 Würfel
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Nur ein Würfel – derjenige, den wir erkannt haben.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
5 Würfel
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
4 Würfel
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
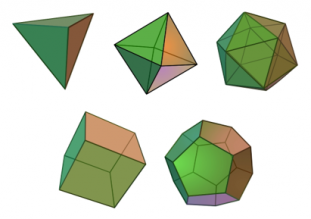
Aus regelmäßigen Sechsecken kann kein regelmäßiges Polyeder gebildet werden. Es gibt insgesamt fünf regelmäßige Polyeder, von denen eines wie erinnerlich das Ikosaeder ist, das wir vorhin in dem Video gesehen haben.
Diese kleinen Sterne heißen „Pentagramm“, was die geometrische Form eines fünfeckigen Sterns aus fünf gleichen Dreiecken bezeichnet. Das Wort „Pentagramm“ kommt aus dem griechischen „pentagrammon“, der Hauptwortform des Eigenschaftsworts „pentagrammos“, das „aus fünf Strichen bestehend“ bedeutet.
Warum ist dieses im Video gezeigte Polyeder, das aus 30 Rauten besteht, kein regelmäßiges Polyeder? Wähle die richtige Antwort.
Weil die Rauten des Polyeders nicht deckungsgleich sind.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Weil die Raute ein Viereck ist und man aus Vierecken kein regelmäßiges Polyeder bilden kann.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Weil die Raute kein regelmäßiges Vieleck ist.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Weil die Raute zwar gleich lange Seiten, aber nicht gleich große Winkel hat.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Weil es nur fünf regelmäßige Polyeder gibt, die alle schon gezeigt wurden, und darunter kein aus Rauten gebildetes regelmäßiges Polyeder war.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Weil die Raute ein Vieleck ist, dessen Seiten nicht gleich lang sind.
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Wie viele Eckpunkte und Seitenflächen hat das regelmäßige Dodekaeder, das wie erinnerlich aus 12 regelmäßigen Fünfecken zusammengesetzt ist? Wähle die richtige Antwort.
20 Eckpunkte und 12 Seitenflächen
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
20 Eckpunkte und 20 Seitenflächen
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
12 Eckpunkte und 12 Seitenflächen
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
12 Eckpunkte und 20 Seitenflächen
כל הכבוד! תשובה נכונה חלקית תשובה נכונה תשובה לא נכונה
Dreidimensionale geometrische Ornamente – ein interaktives Video
הפעל סרטוןעל הפעילות
הבניית ידע
תכנים נוספים שעשויים לעניין אותך
Pocken – ein Albtraum, der (wahrscheinlich) nicht wiederkommt
Vor 40 Jahren erklärte die Weltgesundheitsorganisation die Pocken, eine Krankheit, die Hunderte von Millionen allein im 20. Jahrhundert tötete und wahrscheinlich ganze Kulturen in der Neuen Welt vernichtete, als ausgerottet.
Wie wirkt sich der Klimawandel auf die Vegetation der Erde und auf den Kohlenstoffzyklus aus?
Video über den Einfluss des Klimawandels auf die Vegetation und wie Pflanzen den Kohlenstoffzyklus regeln.
Wer braucht Väter?
Wird ein Mann gebraucht, um Kinder in die Welt zu setzen? Nicht unbedingt, aber auf diese Art und Weise ist es definitiv einfacher.